VITEEE 07 The equation of a directrix of the ellipse (x2/16) (y2/25) = 1 is (A) 3y = 5 (B) y = 5 3y = 25 (D) y = 3 Check Answer and Solutio The length of the focal chord of the ellipse x^2/16y^2/9=1 which is inclined to x axis at an angle 45° is k then 24k/144 is?Get answer The ellipse ((x3)^(2)),(16)(y^(2)),(9)=1 is translated to the right along the x axis by a distance of k unitsThe equation in the new position is ((x3)^(2)),(16)(y^(2)),(9)=1
The Radius Of The Circle Passing Through The Foci Of The Ellipse X 2 16 Y 2 9 Sarthaks Econnect Largest Online Education Community
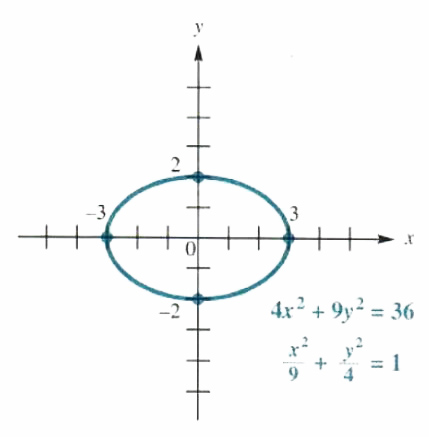
X 2 16 + y 2 9 =1 is equation of an ellipse
X 2 16 + y 2 9 =1 is equation of an ellipse- Problem Statement CE Board May 1993 The length of the latus rectum for the ellipse x^2/64 y^2/16 = 1 is equal to?The best guess to the formula using knowledge of the general formula for an ellipse is x^2/16 y^2/9 = 1 (a) An ellipse is reflectively symmetrical across both the major and minor axis So if you can get the area of the ellipse in a quadrant, then multiplying that area by 4 would give the total area of the ellipse




Find The Standard Form Of The Equation Of The Ellipse Chegg Com
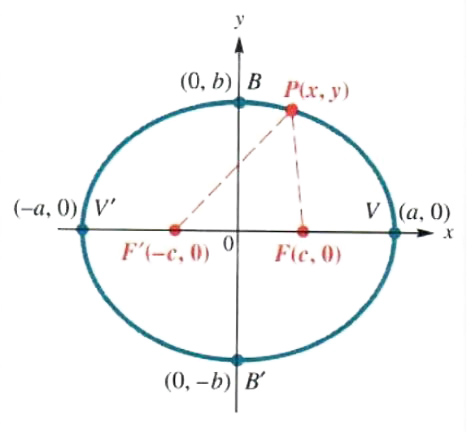
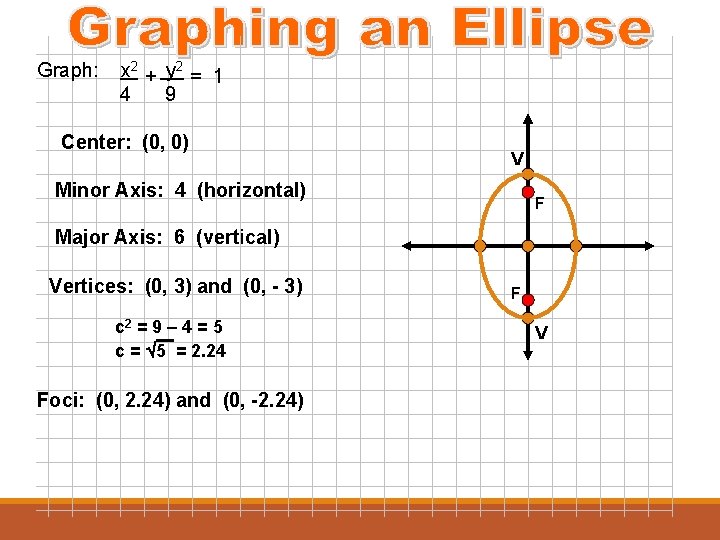
Since a = b in the ellipse below, this ellipse is actually a circle whose standard form equation is x² y² = 9 Graph of Ellipse from the Equation The problems below provide practice creating the graph of an ellipse from the equation of the ellipse An Ellipse comprises two axes They are the major axis and minor axis If the length of semimajor axis = a and length of semiminor axis = b, then 1 Area of the Ellipse = πab 2 Perimeter of the Ellipse = 2π√a2 b2 2 3 Equation of the Ellipse in standard form = This is called the standard form of the equation of an ellipse, assuming that the ellipse is centered at (0, 0) To sketch a graph of an ellipse with the equation \(\ \frac{x^{2}}{a^{2}}\frac{y^{2}}{b^{2}}=1\), start by plotting the four axes intercepts, which are easy to find by plugging in 0 for x and then for y
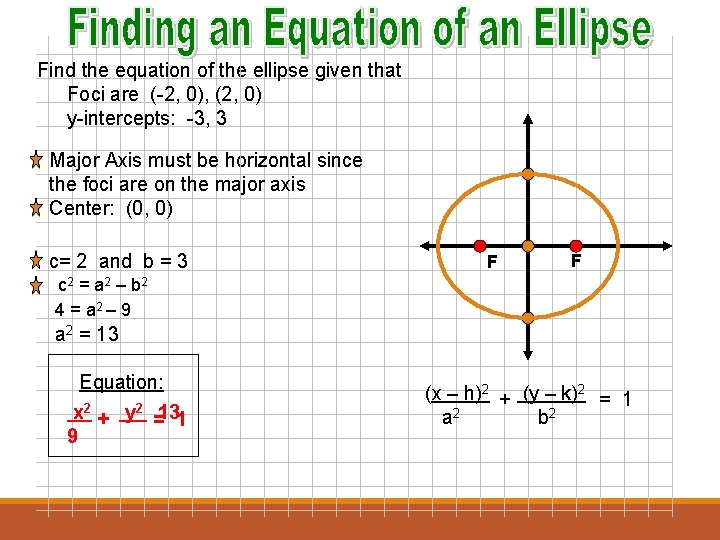
The length of the major axis of an ellipse is units and its foci are (±5√3, 0) Find the equation of the ellipse asked in Ellipse by RahulYadav (530k points) ellipse;As we know thatDirector circle of the ellipse a2x2 b2y2 = 1 is x2 y2 = a2 b2So the director circle of 16x2 9y2 = 1 is x2 y2 = 169 x2 y2 = 25Equation of an Ellipse An ellipse is a conic section, formed by the intersection of a plane with a right circular cone The standard form for the equation of the ellipse is latex\displaystyle{\frac{\left(xh\right)^2}{a^2} \frac{\left(yk\right)^2}{b^2} = 1}/latex if the ellipse is oriented horizontally, and
C is the centre of the ellipse x^2/16 y^2/9 =1 and A and B are 2 points on the ellipse such that angle ACB = 90 and 1/CA^2 1/CB^2=(a/b)^2Tangents PA and PB are drawn to the ellipse `x^2/16 y^2/9=1` from the point P(0, 5) Area of triangle PAB is equal toThe given equation of the ellipse, `x^2/16 y^2/9 = 1` can be represented as It can be observed that the ellipse is symmetrical about x axis and y axis ∴ Area bounded by ellipse
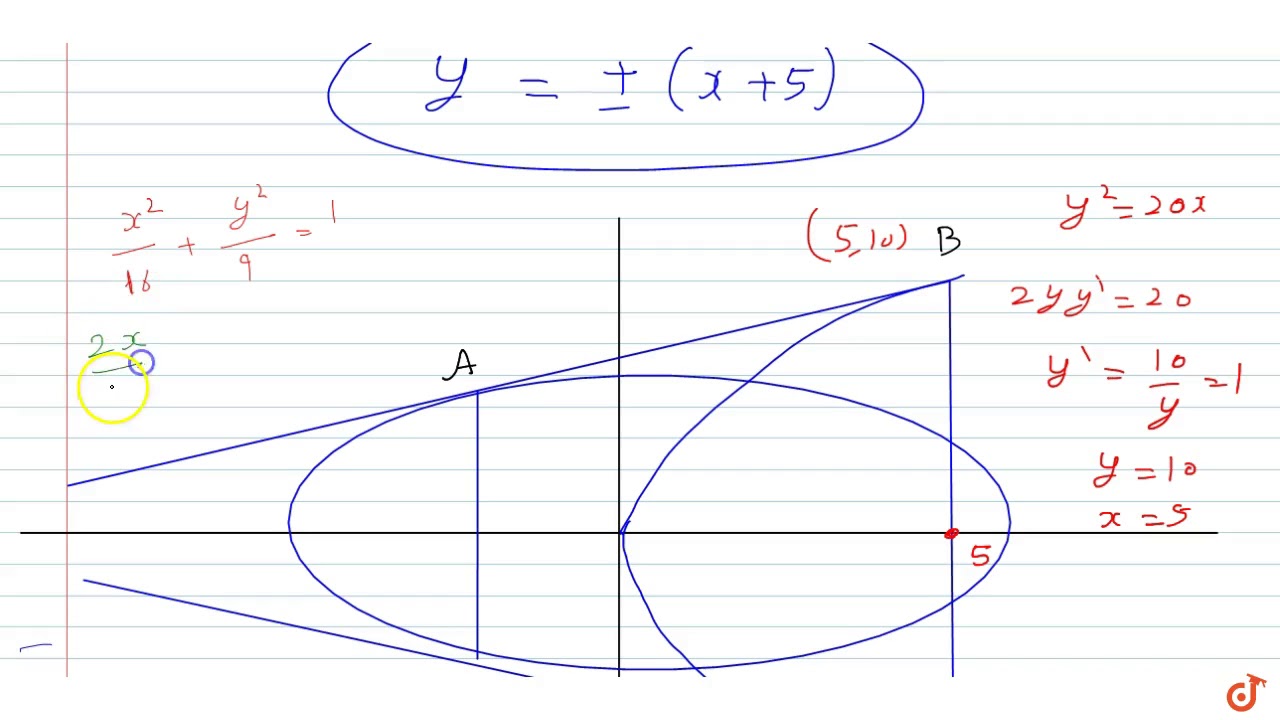



Consider The Parabola Y 2 x Ellipse X 2 16 Y 2 9 1 And Hyperbola X 2 29 Y 2 4 1 The E Youtube




Ex 11 3 5 X2 49 Y2 36 1 Find Foci Eccentricity Ex 11 3
Solved The Equation X 2 16 Y 2 9 1 Defines An Ellipse Chegg Com For more information and source, see on this link https//wwwcheggcom/homeworkhelp/questionsandanswers/equationx216y291definesellipsegraphedexcerciseapproximateareaellipsegettoq584The equation of the circle passing through the foci of the ellipse x ^2/16 y ^2/9 = 1 , and having centre at (0,3) isFree Ellipse calculator Calculate ellipse area, center, radius, foci, vertice and eccentricity stepbystep This website uses cookies to ensure you get the best experience ellipseequationcalculator 9x^{2}16y^{2}=144 en Related Symbolab blog posts Practice, practice, practice




Solution What Is The Equation Of The Asymptote Of The Hyperbola X 2 9 Y




C O N I C S E C T I O N S Part 2 The Circle Circle Ellipse X H 2 Y K 2 R 2 Ellipse X Ypoints On The Circle H Kthe Center Of The Circle Rthe Ppt Download
Algebra Graph (x^2)/16 (y^2)/9=1 x2 16 y2 9 = 1 x 2 16 y 2 9 = 1 Simplify each term in the equation in order to set the right side equal to 1 1 The standard form of an ellipse or hyperbola requires the right side of the equation be 1 1 x2 16 y2 9 = 1 x 2 16 y 2 9 = 1 This is the form of an ellipse Explanation ellipse is (x2/16) (y2/9) = 1 here a2 = 16 and b2 = 9 Now b2 = a2(1 – e2) ⇒ (9/16) = 1 – e2 ⇒ e2 = 1 – (9/16) = (7/16) ∴ e = ± (√7/4) ∴ Foci are (√7, 0) and (– √7, 0) Centre of circle is at (0, 3) and it passes through radius I need help finding the function y = f(x) that gives the curve bounding the top of the ellipse The equation of the ellipse is x^2/16 y^2/9 = 1 I'm just not sure even where to start Thanks for any help




If E 1 Is The Eccentricity Of The Ellipse X 2 16 Y 2 25 1 And E 2 Is The Eccentricity Of Youtube



30 Ellipses 1 An Ellipse Is A Set
Solve the equation for an ellipse for y Assume that y > 0 y^2/a^2 x^2/b^2 = 1 2 See answers Brainly User Brainly User Multiply each term by a^2b^2b^2y^2 a^2x^2 = a^2b^2 subtract a^2x^2 from both sides b^2y^2 = a^2b^2 a^2x^2 Now divide both sides by b^2 An equation of an ellipse is given x^2/25 y^2/9 = 1 (a) Find the vertices, foci, and eccentricity of the ellipse vertex x, y (smaller value), vertex x,y (larger value) focus x,y (smaller) focus x,y (larger) (b) Determine the length of the major axis (c) Determine the length of the minor axis (d) sketch the graph Who are the experts The equation is ( x − h)2 a2 ( y − k)2 b2 = 1 and when a > b, the major axis is horizontal so the distance from the center to the vertex is a When b > a, the major axis is vertical so the distance from the center to the vertex is b Definition 3 Standard Form of the Equation an Ellipse with Center (h, k)
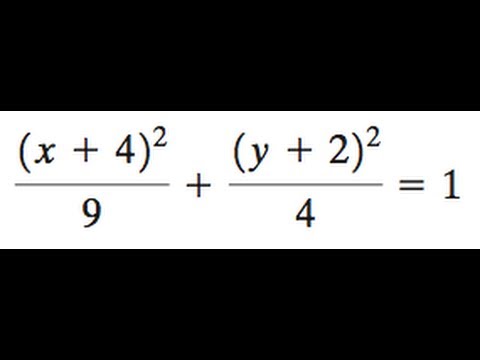



X 4 2 9 Y 2 2 4 1 For The Ellipse Find The Center Foci And Vertices Graph The Equation Youtube




Find The Standard Form Of The Equation Of The Ellipse Chegg Com
A point on the ellipse x^2/16 y^2/9 = 1 at a distance equal to the mean of the length of the semi major axis and semi minor axis from the center isThe standard form of an ellipse or hyperbola requires the right side of the equation be 1 1 x2 16 y2 12 = 1 x 2 16 y 2 12 = 1 This is the form of an ellipse Use this form to determine the values used to find the center along with the major and minor axis of the ellipse (x h)2 a2 (yTo graph an ellipse, visit the ellipse graphing calculator (choose the "Implicit" option) Enter the information you have and skip unknown values Enter the equation of an ellipse In any form you want `x^24y^2=1`, `x^2/9y^2/16=1`, etc Enter the center ( , ) Enter the first focus ( , ) Enter the second focus



Solve Ellipse And Hyperbola Step By Step Math Problem Solver




What Is The Equation Of The Circle That Passes Through The Foci Of An Ellipse Given By The Equation X 2 16 Y 2 9 1 And Has Its Centre At 0 3 Quora
I am a little lost up until this point and the formula doesn't seem to be going in the direction it needs to so that it will become the area of an ellipse I feel like I made a mistake somewhere along the wayAnswer to Find the slope of the tangent line to the ellipse x^2 / 16 y^2 / 9 = 1 at the point (x, y) By signing up, you'll get thousands ofThe equation x^2/16 y^2/9=1 defines and ellipse a) Find the function y=f(x) that gives the curve bounding the top of the ellipse b) use ?x = 1 and midpoints to approximate the area of the part of the ellipse lying in the first quadrant




Conic Sections



Solve Ellipse And Hyperbola Step By Step Math Problem Solver
The best guess to the formula using knowledge of the general formula for an ellipse is x^2/16 y^2/9 = 1 (a) An ellipse is reflectively symmetrical across both the major and minor axis So if you can get the area of the ellipse in a quadrant, then multiplying that area by 4 would give the total area of the ellipse So the factor of 4 isProblem Answer The length of the latus rectum of the ellipse is 4 unitsOriginally Answered The equation of the circle passing through the Foci of the ellipse x^2/16 y^2/9 = 1 and having a centre at (0,3) is ?



If E1 Is The Eccentricity Of The Ellipse X 2 16 Y 2 25 1 And E2 Is The Eccentricity Of The Hyperbola Passing Through The Foci Sarthaks Econnect Largest Online Education Community



30 Ellipses 1 An Ellipse Is A Set
Please select the best answer from the choices provided BLets break this question down To find the equation of the circle, you have been given the center, so put those values in the general equation of the circle x^2 (y3)^2=r^2, r is the radius Ex 114, 1Find the coordinates of the foci and the vertices, the eccentricity, and the length of the latus rectum of the hyperbola x2 16 y2 9 = 1Given equation is 2 16 2 9 = 1The above equation is of the form 2 2 2 2 = 1So axis of



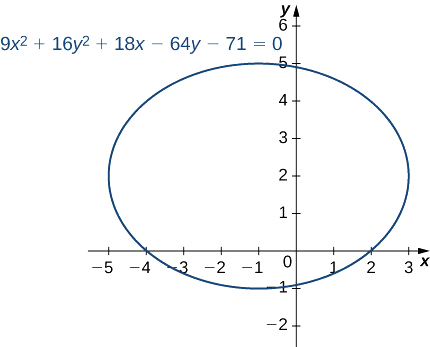
Solution Hi Can You Please Help Me With This Question Graph The Equation Equal To 9x 2 16y 2 36x 32y 92 0 And Find The Vertix Focus Point And Axis Of Symmetry Thank You All Your Help



Find The Area Of The Region Bounded By The Ellipse X 2 16 Y 2 9 1 Sarthaks Econnect Largest Online Education Community
Find the equations of the tangents to the ellipse `x^2/16 y^2/9` = 1, making equal intercepts on coordinate axes Advertisement Remove all ads Solution Show Solution The equation of the ellipse is `x^2/16 y^2/9` = 1 Comparing with `x^2/"a"^2 y^2/"b"^2` = 1, we get, a 2 = 16, b 2 = 9 Let the required tangent make intercept c on each axisThe equation x 2 16 y 2 9 1 defines an ellipse which is graphed above In this The equation x 2 16 y 2 9 1 defines an ellipse which School University of Washington;16 E is the ellipse x 2 16 y 2 9 1 and P 4 cos θ 3 sin θ is a point onE with from HSC 1 at Alma College




Consider The Ellipsoid Given By The Equation X 2 16 Chegg Com




P Is The Point On The Ellipse Isx 2 16 Y 2 9 1 And Q Is The C
X 2 16 Y 2 9 1 Is Equation Of An Ellipse The Smaller Region Bounded By The Ellipse X 2 16 Y 2 9 1 And A Straight Line 3x 4y 12 What Should Be The Area Of That Smaller Region Quora For more information and source, see on this link httpsFinding the points of intersection x^2 y^2 = r^2 — Eq 1 x^2/16 y^2/9 = 1 — Eq 2 from Eq 1 x^2 = r^2 y^2 — substitute this in Eq 2 and find the value of y Therefore, y = or sqrt((144–9*r^2)/7) — substitute this in Eq 1 to find value ofX^2/16 y^2/9 = 1 Find the equation of the ellipse with the following properties The ellipse with foci at (0, 6) and (0, 6);




Ex 11 3 3 X2 16 Y2 9 1 Find Vertices Length Of Minor Axis



1
Type Homework Help Uploaded By luckystar381 Pages 19 Ratings 67% (3) 2 out of 3 people found this document helpful; x^2/16y^2/9=1 a^2=16 b^2=9 The center is (0,0) The xaxis is the major axis We know this because the x^2 term has the larger denominator We find the foci using the following equation and solving for c c^2=a^2b^2 c^2=169 c^2=7 c=sqrt(7) The coordinates for the foci are (c,0) > (sqrt(7),0)Click here 👆 to get an answer to your question ️ x^2/16y^2/9 =1 is equation of an ellipse (true or false) llalamrit561 llalamrit561 Math Secondary School answered X^2/16y^2/9 =1 is equation of an ellipse (true or false) 2



1



If E Is The Eccentricity Of The Ellipse X 2 25 Y 2 9 1 And If E2 Is The Eccentricity Of The Hyperbola 9x 2 16y 2 144 Then E1e2 Is Sarthaks Econnect Largest Online Education Community
Yintercepts (0, 8) and (0, 8) The foci of a hyperbola coincide with the foci of the ellipse x^2/25 y^2/9 = 1 Find the equation of the hyperbola, asked in Mathematics by Sindhu01 (The standard form of the equation of an ellipse with center (0,0) ( 0, 0) and major axis parallel to the y axis is x2 b2 y2 a2 =1 x 2 b 2 y 2 a 2 = 1 where a >b a > b the length of the major axis is 2a 2 a the coordinates of the vertices are (0,±a) ( 0, ± a) the length of the minor axis is 2b 2 b




Write The Equation Of An Ellipse In Standard Form Chegg Com




Bounded Area Of Ellipse Find The Equation Of The Region Bounded By The Ellipse X 2 16 Y 2 9 1 Youtube
Then, the equation of rupak26 rupak26 Math Secondary School a chord of the ellipse x^2/16y^2/9=1 passing through the positive focus subtends an angle of 90 at centre the coordinates of point at where it goes on to intersect the y axis 1 2 See answers The standard form of the equation for an ellipse is given by #(xx_c)^2/a^2 (yy_c)^2/b^2 = 1# with the point #(x_c, y_c)# representing the center, the value #a# representing the horizontal semiaxis length, and the value #b# representing the vertical semiaxis lengthRecent Posts A car starts from rest, if the acceleration becomes 60m/s² after seconds, calculate the final velocity of the car A pure sample of a compound on combustion analysis gave 361 mg of CO2 and 147mg of H2O if the




The Foci Of The Hyperbola X 2 16 Y 2 9 1 Is




Mp Board Class 11th Maths Important Questions Chapter 11 Conic Sections Mp Board Solutions
The equation of the ellipse is (x 2 / 16) (y 2 / 9) = 1 a = 4 and b = 3 Eccentricity = e = √1 – (b 2 / a 2) = √1 – (9 / 16) = √7 / 16 = √7 / 4 Foci of the ellipse are (± ae, 0) = (± √7, 0) Radius of the required circle = √ (√7 – 0) 2 (0 – 3) 2 = √7 9 = √16 = 4If the equation of an ellipse is in standard form and the denominators are equal, then the ellipse is a circle Please select the best answer from the choices provided T Which is the graph of x^2/16 y^2/9 = 1 ?Course Title MATH 125;




Ex 11 3 3 X2 16 Y2 9 1 Find Vertices Length Of Minor Axis




Misc 8 Find Area Of Smaller Region Bounded By Ellipse Miscellaneou
The equation of a line through the intersection of lines x = 0 and y = 0 and through the point (2, 2), is The equation of a straight line passing through (3, 2) and cutting an intercept equal in magnitude but opposite in signs from the axes is given by The equation of an ellipse whose eccentricity is 1/ 2 and the vertices are (4, 0) and (10A point on the ellipse `x^(2)/16 y^(2)/9 = 1` at a distance equal to the mean of lengths of the semi major and semiminor axis from the centre, is




The Number Of Common Tangents To The Ellipse X 2 16 Y 2 9 1 And The Circle X 2 Y 2 4 Is




Find The Equations Of The Lines With Equal Intercepts On The Axes Which Touch The Ellipse X 2 16 Y 2 9 1



Ellipses



The Equation Of The Circle Passing Through The Foci Of The Ellipse X 2 16 Y 2 9 1 And Sarthaks Econnect Largest Online Education Community



Find The Foci Of The Graph Of X 2 4 Y 2 9 1 Mathskey Com



The Area Of The Region Bounded By The Ellipse X 2 25 Y 2 16 1 Is Sarthaks Econnect Largest Online Education Community



11 5 Conic Sections Mathematics Libretexts
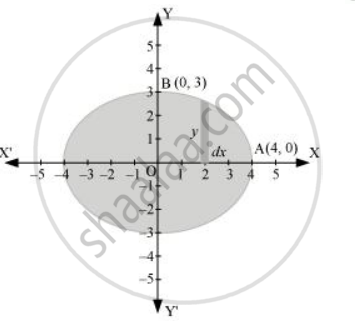



Find The Area Of The Region Bounded By The Ellipse X 2 16 Y 2 9 1 Mathematics Shaalaa Com




Ex 11 4 1 Find Foci Vertices Of Hyperbola X 2 16 Y 2 9 1



What Is The Center Of The Ellipse Math Frac X Y 2 2 9 Frac X Y 2 16 1 Math Quora




Consider The Parabola Y 2 x Ellipse X 2 16 Y 2 9 1 And Hyperbola X 2 29 Y 2 4 1 The Equation Common Tangent To All Of Them Is



Ellipses



Find The Coordinates Of The Foci The Vertices The Length Of Major Axis The Minor Axis X 2 16 Y 2 9 1 Sarthaks Econnect Largest Online Education Community
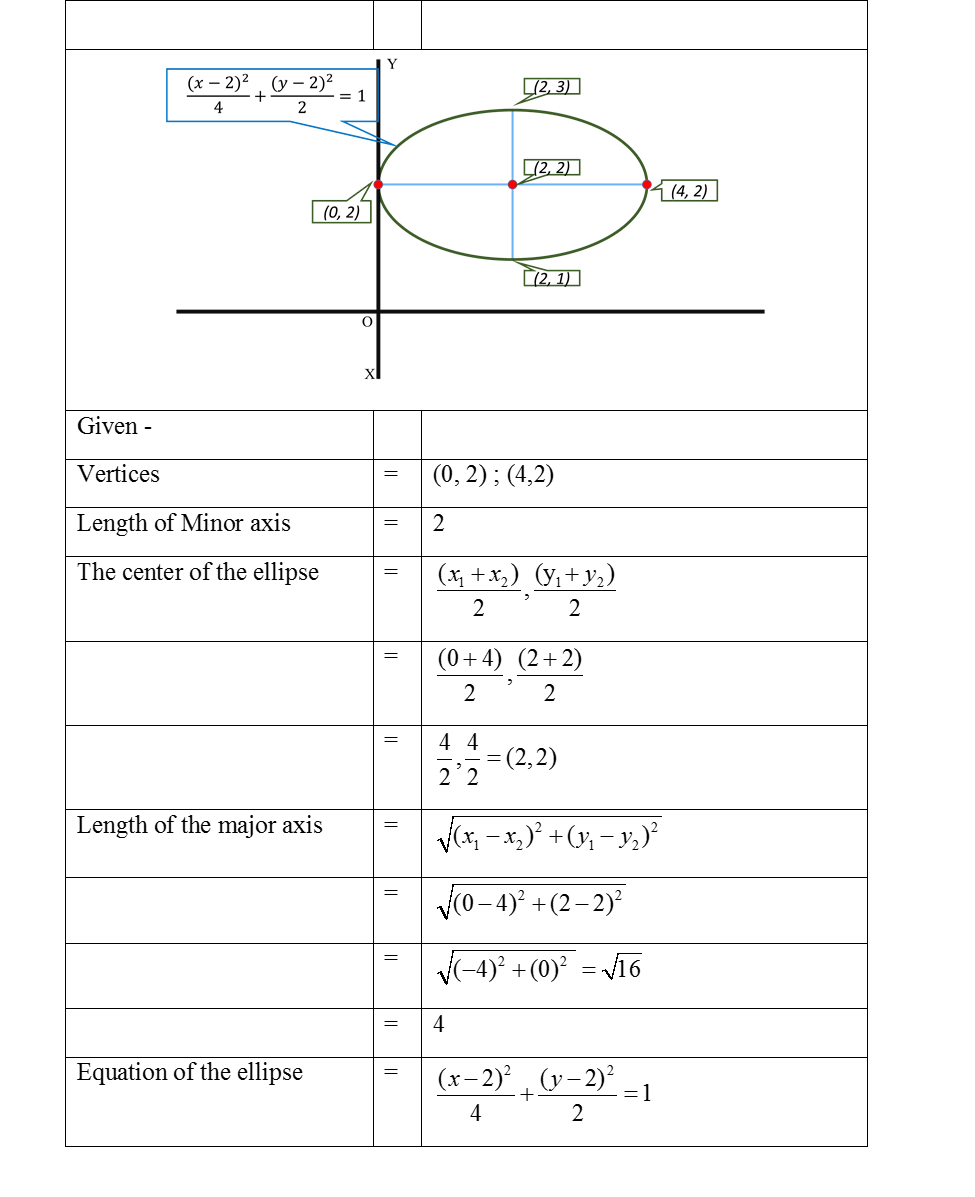



How Do You Write An Equation Of A Ellipse With Vertices 0 2 4 2 And Minor Axis Of Length 2 Socratic




The Ellipse With Foci At 3 0 And 3 0 And Chegg Com
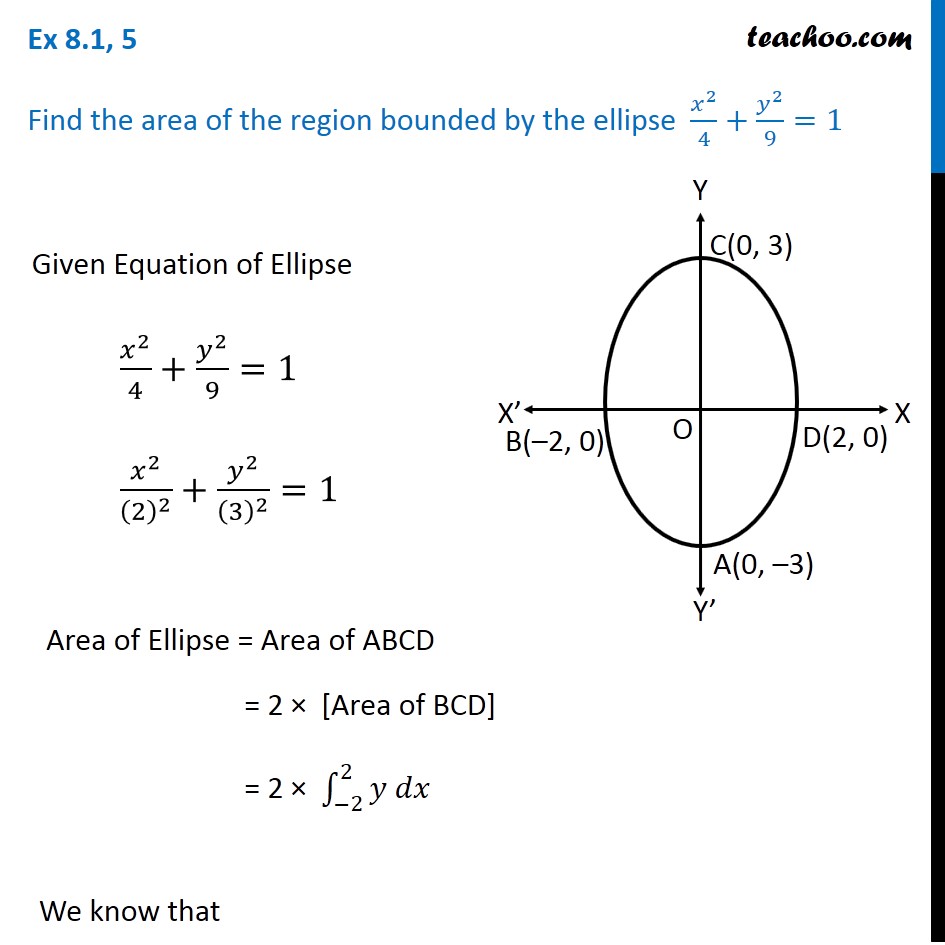



Ex 8 1 5 Find Area By Ellipse X2 4 Y2 9 1 Class 12



30 Ellipses 1 An Ellipse Is A Set



Ex 8 1 5 Find Area By Ellipse X2 4 Y2 9 1 Class 12




Consider The Ellipse X 2 9 Y 2 4 1 And The Parabola Y 2 2x They Intersect At P And Q In The First Andfourth Quadrants Respectively Tangents To The Ellipse At P And Q Intersect The



Ellipses




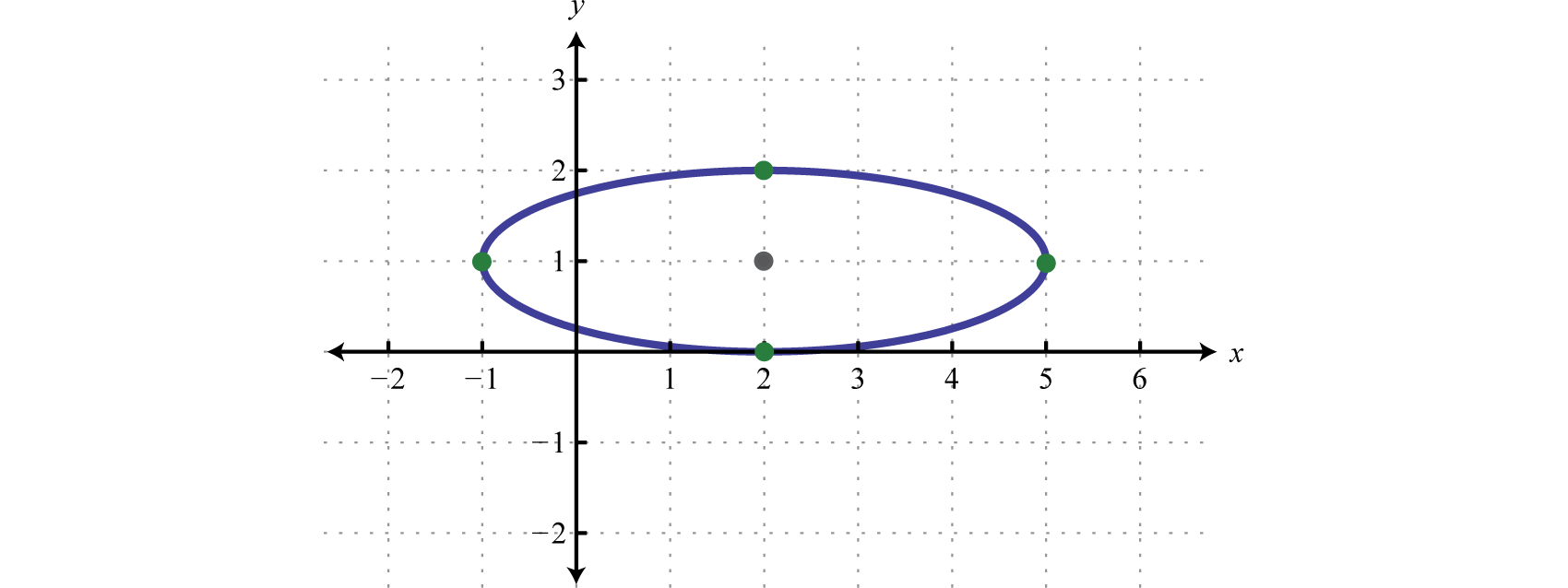
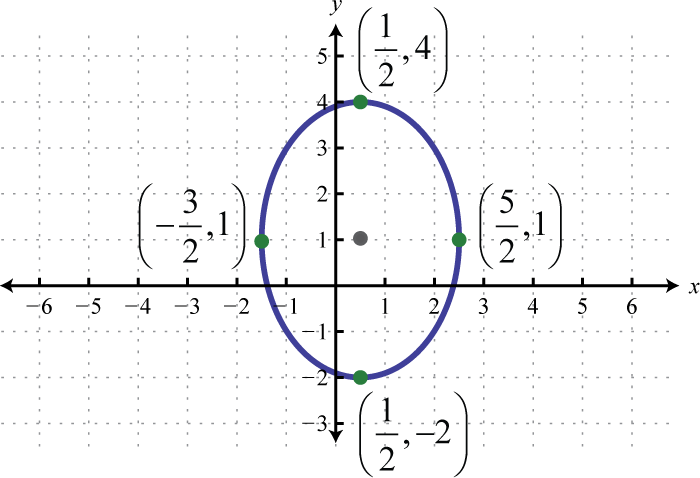
Write The Equation Of The Ellipse Shown In The Graph A X 1 2 4 Y 2 2 9 1b X 1 2 9 Brainly Com




Statement 1 Two Ellipses X 2 16 Y 2 9 1 And X 2 9 Y 2 16 1 Are Congruent Statement 2 X 2 16 Y 2 9 1 And X 2 9 Y 2 16 1 Have Same Eccentricity




6 3 Conic Sections Ellipses Ppt Download



Find Eccentricity Of The Hyperbola X 2 16 Y 2 9 1 Sarthaks Econnect Largest Online Education Community



View Question Help Asap Please
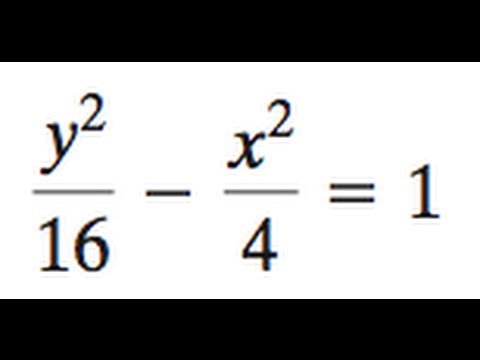



Hyperbola Y 2 16 X 2 4 1 Youtube
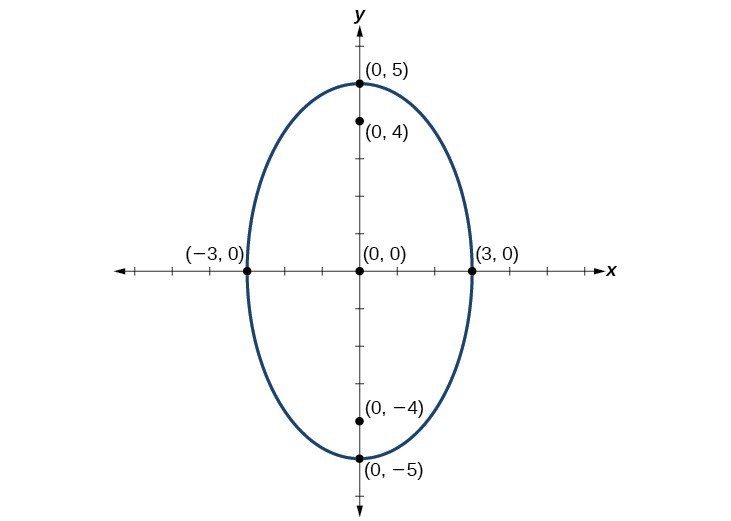



Graphs Of Ellipses College Algebra



If E1 Is The Eccentricity Of The Ellipse X 2 16 Y 2 25 1 And E2 Is The Eccentricity Of The Hyperbola Passing Through The Foci Sarthaks Econnect Largest Online Education Community




Solution The Length Of The Latus Rectum For The Ellipse X 2 64 Y 2 16 1 Is Equal To




A Tangent To The Ellipse X 2 25 Y 2 16 1 At Any Point P Meets The Line X 0 At A Point Q Let R Be The Image Of Q



The Smaller Region Bounded By The Ellipse X 2 16 Y 2 9 1 And A Straight Line 3x 4y 12 What Should Be The Area Of That Smaller Region Quora
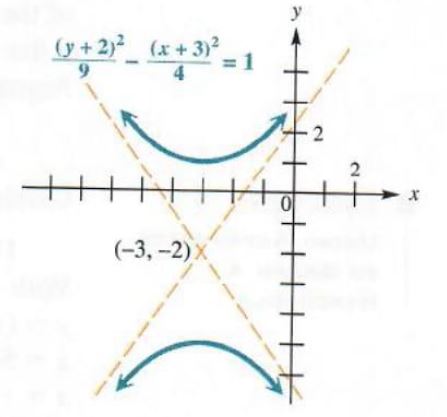



Solve Ellipse And Hyperbola Step By Step Math Problem Solver



Find The Area Of The Region Bounded By The Ellipse X 2 16 Y 2 9 1 Sarthaks Econnect Largest Online Education Community




P Is The Point On The Ellipse Isx 2 16 Y 2 9 1 And Q Is The Corresponding Point On The Auxiliary Circle Of The Ellipse If The Line Joining The Center C To Q Meets The



The Radius Of The Circle Passing Through The Foci Of The Ellipse X 2 16 Y 2 9 Sarthaks Econnect Largest Online Education Community




Find The Area Of The Region Bounded By The Ellipse X 2 16 Y 2 9 1 Mathematics Shaalaa Com
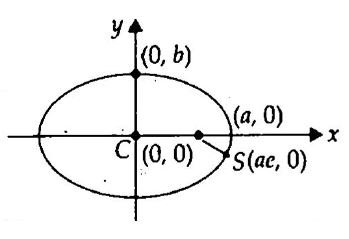



If C Is The Centre Of The Ellipse X2 16 Y2 9 1 And




The Maximum Distance Of The Centre Of The Ellipse X 2 16 Y 2 9 1 From The Chord Of Contact Of Mutually Perpendicular Tangents Of The Ellipse Is



30 Ellipses 1 An Ellipse Is A Set




Section 11 6 Conic Sections Ppt Download




X 2 16 Y 2 9 1 Novocom Top




Section 7 3 The Ellipse Ellipse A Set Of Points In A Plane Whose Distances From Two Fixed Points Is A Constant Ppt Download



Q Tbn And9gcrt9kzolvvf1dqbohybtl30n4ovatqoqhm3locajx Quufi9fnw Usqp Cau




Ex 8 1 4 Find Area Bounded By Ellipse X2 16 Y2 9 1



What Is The Center Of The Ellipse Math Frac X Y 2 2 9 Frac X Y 2 16 1 Math Quora



30 Ellipses 1 An Ellipse Is A Set




Example 9 X2 25 Y2 9 1 Find Foci Vertices Eccentricity



The Smaller Region Bounded By The Ellipse X 2 16 Y 2 9 1 And A Straight Line 3x 4y 12 What Should Be The Area Of That Smaller Region Quora




Ex 11 3 3 X2 16 Y2 9 1 Find Vertices Length Of Minor Axis




Sketch The Graph Of A Hyperbola Given That Its Chegg Com




Ex 8 1 Q4 Find The Area Of The Region Bounded By The Ellipse X 2 16 Y 2 9 1



The Minimum Distance Of The Center Of The Ellipse Dfracx216 Dfracy291 Class 11 Maths Cbse



Hyperbolas




Statement 1 Two Ellipses X 2 16 Y 2 9 1 And X 2 9 Y 2 16 1 Are Congruent Statement 2 X 2 16 Y 2 9 1 And X 2 9 Y 2 16 1 Have Same Eccentricity




Find The Equation Of Normal To The Hyperbola X 2 16 Y 2 9 1 At 4 0



What Does X 4 2 4 Y 7 2 9 1 Represent Socratic



The Area Of The Region Bounded By The Ellipse X2 25 Y2 16 1 Is Studyrankersonline



Ellipses And Hyperbolae




Solution What Is The Equation Of The Asymptote Of The Hyperbola X 2 9 Y 2 4 1




7 03 Ellipses And Circles
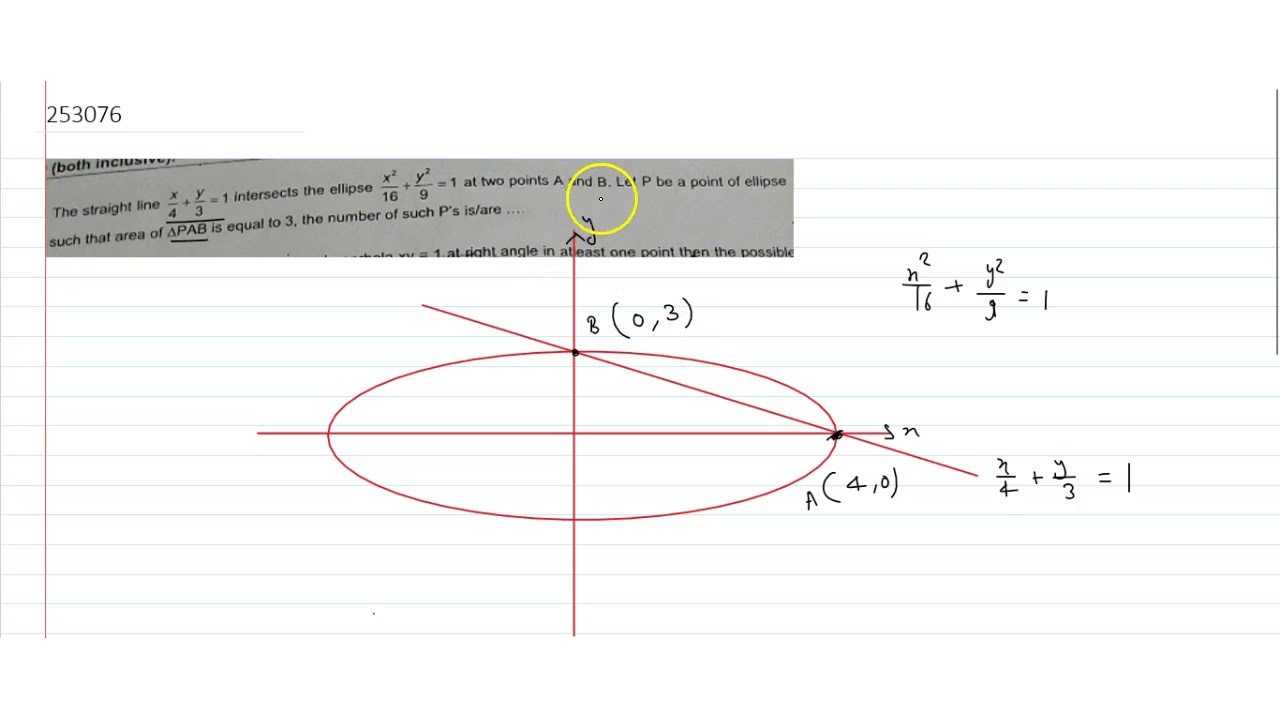



The Straight Line X 4 Y 3 1 Intersects The Ellipse X 2 16 Y 2 9 1 At Two Points A And Youtube




Ex 8 1 4 Find Area Bounded By Ellipse X2 16 Y2 9 1



Content The Concept Of A Function




If E 1 Is The Eccentricity Of The Ellipse X 2 16 Y 2 25 1 And E 2 Is The Eccentricity Of The Hyperbola Passing Through The Foci Of The Ellipse And E 1 E 2 1 Then Equation Of The Hyperbola
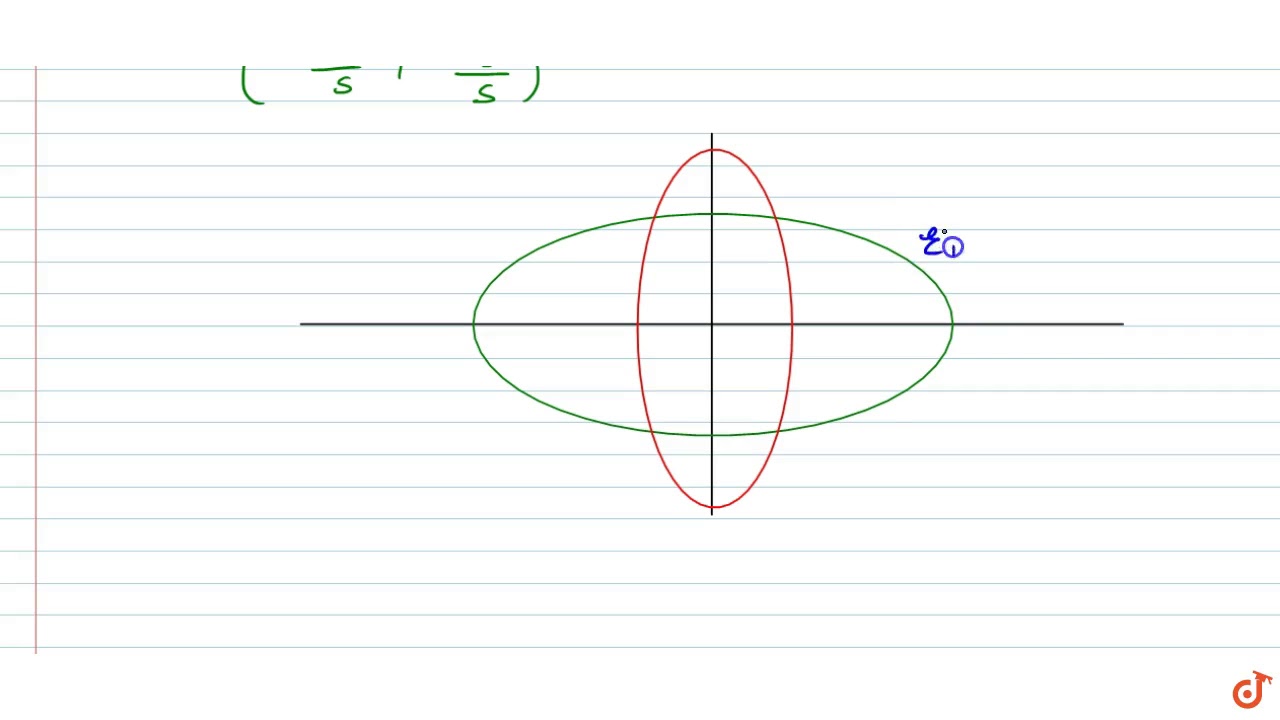



The Length Of Common Tangent To The Ellipses X 2 16 Y 2 9 1 And X 2 9 Y 2 16 1 Is Youtube
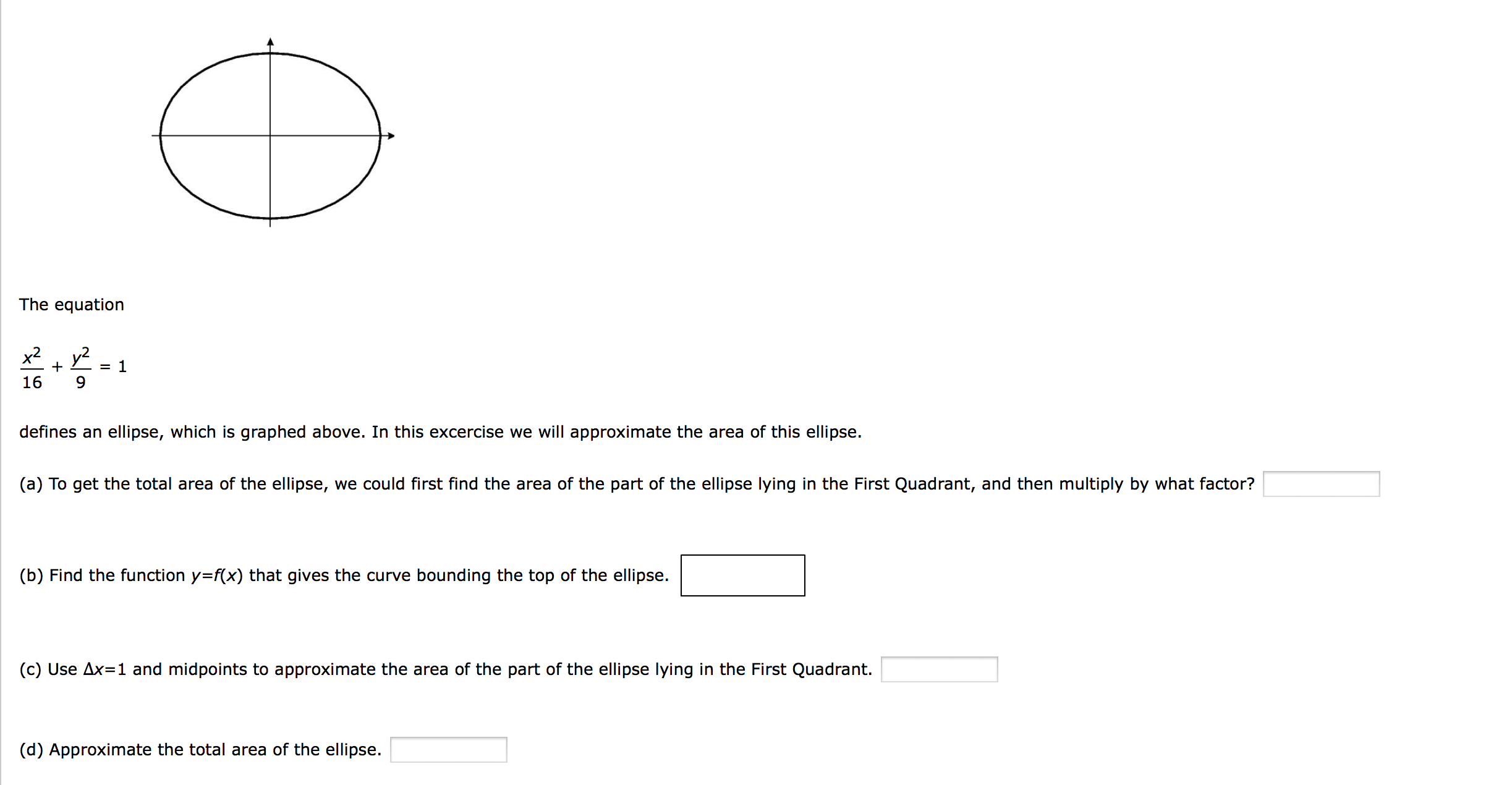



The Equation X 2 16 Y 2 9 1 Defines An Ellipse Chegg Com




The Equation Of The Ellipse Shown Is X 4 Y 3 1 Chegg Com




If A Hyperbola Passes Through The Foci Of The Ellipse X 2 25 Y 2 16 1 Its Transverse And Conjugate Axes Coincide Respectively With The Major And Minor Axes Of The Ellipse And If The Product



Q Tbn And9gcsdcv1zjbhdzehbinsqbnagi9sehwn4ni6kcbl Tsmk1kcjxlmr Usqp Cau
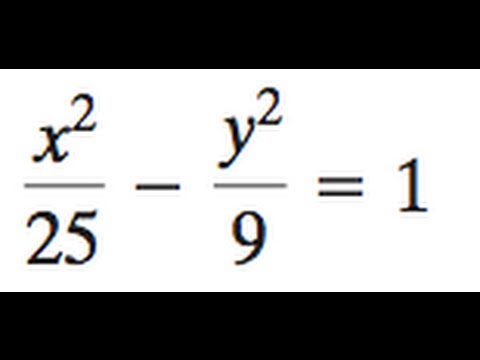



Hyperbola X 2 25 Y 2 9 1 Youtube




Ex 8 1 4 Find Area Bounded By Ellipse X2 16 Y2 9 1



Solution Y 2 16 X 2 9 1 Identify The Curve Find The Center Asymptotes Foci Then Sketch The Curve




Consider An Ellipse X 2 25 Y 2 9 1 With Centre C And A Point P On It With Eccentric Angle Youtube




If The Equation Of The Curve On Reflection Of The Ellipse Frac X 4 2 16 Frac Y 3 2 9 1 About The Line X Y 2 0 Is 16 X 2 9 Y 2 K 1 X 36 Y K 2 0 Then Left K 1 K 2 Right 66




Find The Equation Of Normal To The Hyperbola X 2 16 Y 2 9 1 At 4 0 Youtube




Undefined Intermediate Algebra Openstax Cnx


