This answer is useful 1 This answer is not useful Show activity on this post ~p→ (q→r) p v (q→r) p v (~q v r) p v ~q v r q→ (p v r) ~q v (p v r) ~q v p v r p v ~q v r Here I am using the rule that p→q ~p v q and the fact that disjunction is associative and commutative Share(p∨q) → r ≡¬(p∨q)∨r by implication law ≡(¬p∧¬q)∨r by de Morgan's laws ≡(¬p∨r)∧(¬q∨r) by distributive laws ≡(p→ r)∧(q→ r) by implication laws twice 5 (0 points), page 35, problem 24 (p→ q)∨(p→ r) ≡(¬p∨q)∨(¬p∨r) by implication law, twice ≡(¬p∨¬p)∨(q∨r) byUsing truth tables, verify whether implication is associative, ie, whether p ⇒ (q ⇒ r) ≡ (p ⇒ q) ⇒ r Close 0 Posted by u/deleted 2 months ago Using truth tables, verify whether implication is associative, ie, whether p ⇒ (q ⇒ r) ≡ (p ⇒ q) ⇒ r You just set the truth values for $(q \implies r)$ and $(p \implies
The Foundations Logic And Proofs Ppt Download
P → q ∨ r p ↔ r ∧ q p ∧ q ∨ ¬r p ∨ q ↔ p ∧ r
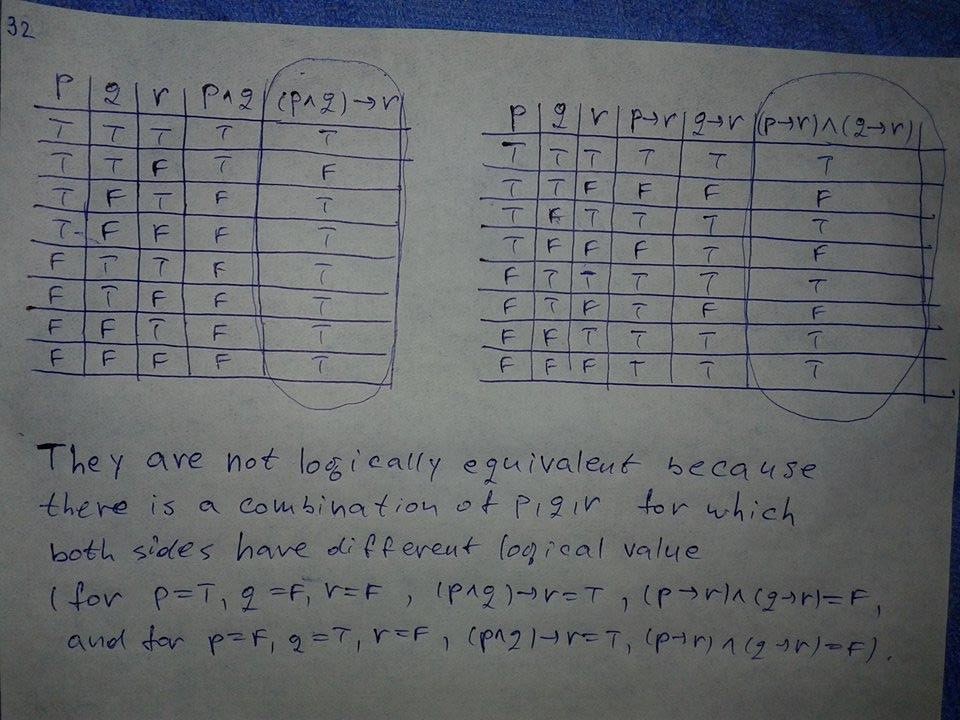
P → q ∨ r p ↔ r ∧ q p ∧ q ∨ ¬r p ∨ q ↔ p ∧ r-Solution The correct option is D p ∧ (∼ q ∧∼ r) We know that, ∼(p → q) ≡ p ∧ (∼ q) Also, negation of (q ∨ r) is (∼ q∧∼ r) So, ∼ (p →(q ∨ r)) ≡ p ∧(∼q∧∼r) Mathematics Suggest Corrections 3 Similar questions Q Negation of the statement ∼p→(q∨r) is Mathematics Q The negation of q ∨ ∼(p∧r) is ___ Mathematics View More People also searched for Q Correct answer Show that (p → r) ∧ (q → r) and (p ∨ q) → r are logically equivalent Sikademy Correct answer Show that (p → r) ∧ (q → r) and (p ∨ q) → r are logically equivalent Sikademy a ≡ 11 (mod 19) and b ≡ 3 (mod 19) Find an integer c with 0≤c≤18 such that (a)c≡13a(mod 19) (b)c≡8b(mod 19) (c)c≡a




Use Truth Tables To Verify The Associative Laws A P Q Quizlet
This sort of logical proof can easily be written in straight term mode though example (p q r Prop) (p ∨ q) ∧ (p ∨ r) → p ∨ (q ∧ r) = λ hpq, hpr , orelim hpq orinl $ λ hq, orelim hpr orinl $ λ hr, orinr hq, hr The "duplication" now is just the fact that the function orinl shows up twice My feeling is that because p但它们是有联系的, p 和 q 是语法等价的,当且仅当 p ↔ q 是一个 定理 ,而 p 和 q 是语义等价的, 当且仅当 p ↔ q 是 重言式 。 逻辑等价有时表示为 p ≡ q 或 p ⇔ q 。 但是,后者记号也用于实质等价。 逻辑等价公式 包括 蕴涵 的逻辑等价: p→q≡﹁p∨q p→q≡﹁q→﹁p p∨q≡﹁p→q p∧q≡﹁ (p→﹁q) ﹁ (p→q)≡p∧﹁q (p→q)∧ (p→r)≡p→ (q∧r) (p→q)∨ (p→r)≡p→ (q∨r) (p→r)∧ (q→r)≡ (p∨q)→r (p→r)∨Answer (1 of 2) Question originally answered What is the truth table for (p>q) ^ (q>r)> (p>r)?
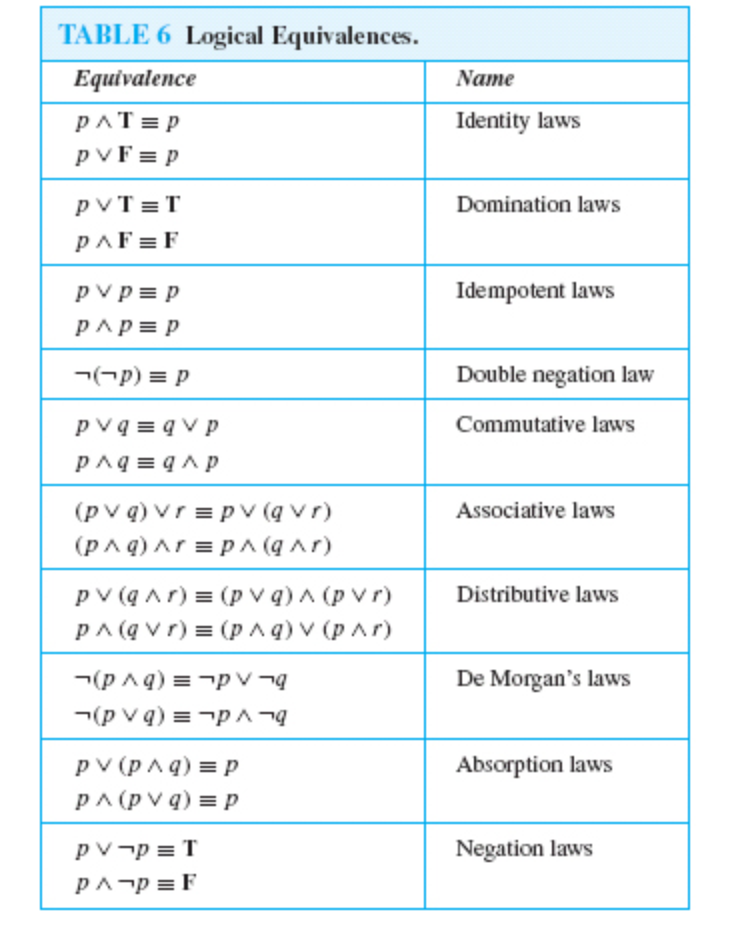
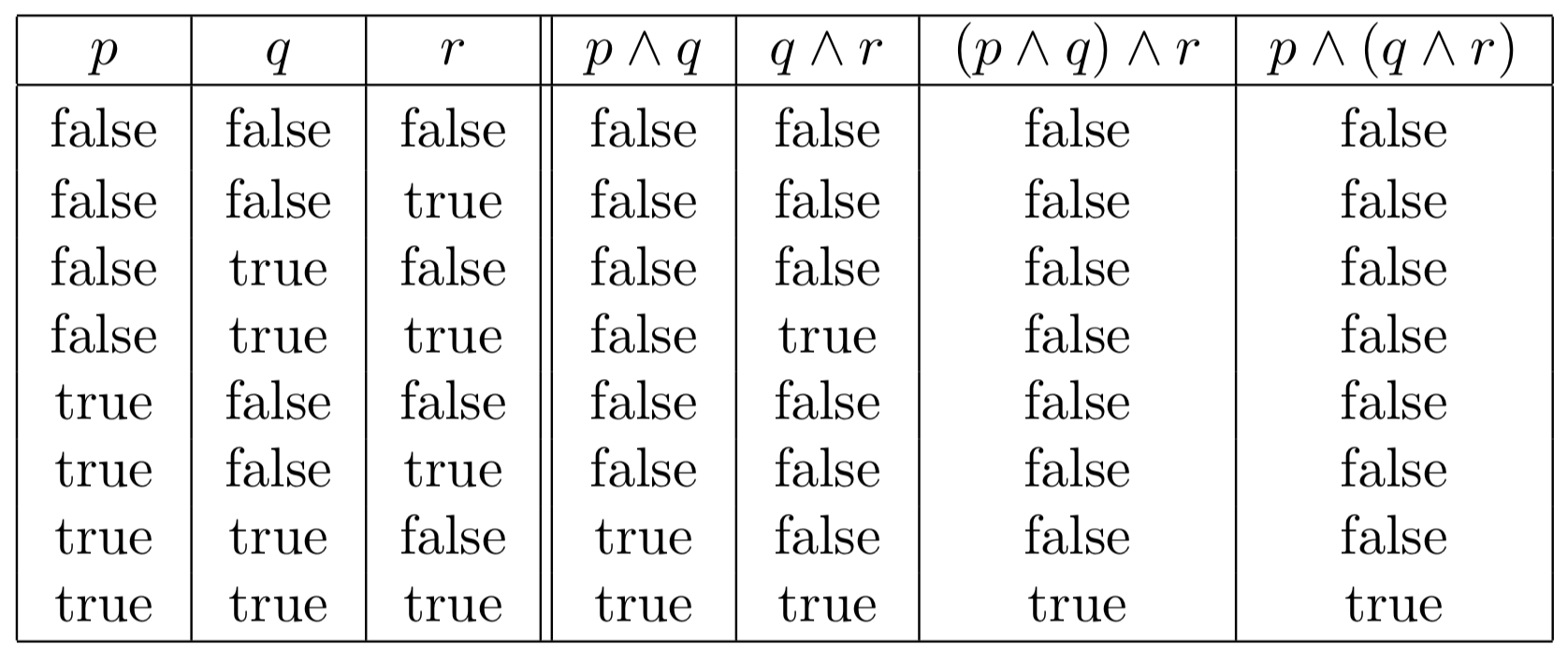
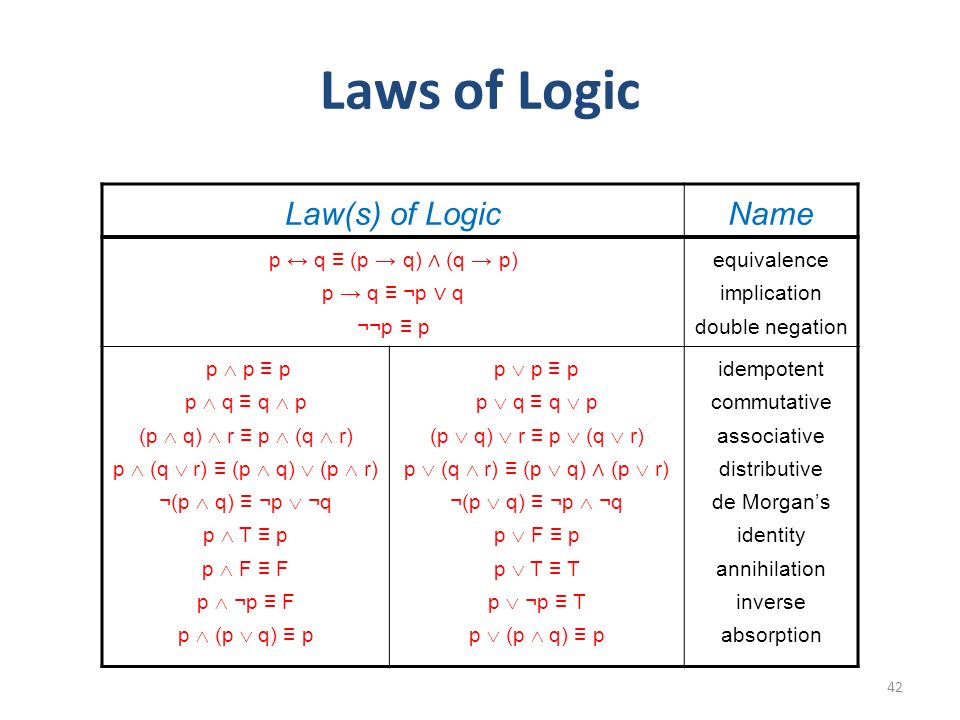
(p ∧ q) ∧ r ≡ p ∧ (q ∧ r) p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r) p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r) Double Negation Law We have ¬(¬p)≡p p ¬p ¬(¬p) F T F T F T Logical Equivalences You find many more logical equivalences listed in Table 6 on page 27Different ways to answer the above question 1 By means of the Truth Table 2 By means of derivation 3 By formulating it as logical equivalence, that is, as a "proof" MSU/CSE 260 Fall 09 24 Is (¬ (p ∧q)) →(¬ p ∨q) ≡(¬ p ∨q) ?In this case, the truth values for (~r∧(p→~q))→p and r∨p are exactly the same, so we can conclude that the two statements are equivalent (~r∧(p→~q))→p≡r∨p So, if we ever encounter(~r∧(p→~q))→p, we can replace it with r∨p without changing the logical meaning of the statement!
Find stepbystep Discrete math solutions and your answer to the following textbook question Use truth tables to verify the associative laws a) (p ∨ q) ∨ r ≡ p ∨ (q ∨ r) b) (p ∧ q) ∧ r ≡ p ∧ (q ∧ r) question_answer Answers (1) To show (pq) is a factor of f (b), we find the zero of the binomial (p q) Therefore, (p q) is a factor of p 2 (qr) q 2 (rp) r 2 (pq) The given expression is a cyclic expression in p, q and r, so the factors of the expression are also cyclic Therefore (q r), (r p) are the other factors of the This answer is useful 1 This answer is not useful Show activity on this post LHS ( (p → q) ∨ (¬p → r)) → (q ∨ r) ≡ (¬p v q) v (p v r) → (q v r) Implication Law and truth table ≡ ¬ (¬p v q) v (p v r) v (q v r) Implication Law ≡ ¬ (¬p v q) ∧ ¬ (p v r) v (q v r) De Morgan Law ≡ (¬ (¬p) ∧ ¬q) ∧ (¬p ∧ ¬r) v (q v r) De Morgan Law




Using The Truth Table Prove The Following Logical Equivalence P Q R P Q P R



By Using Logic Laws Can You Show That The Proposition P Q P Q Is A Contradiction Quora
Use the truth table to determine whether the statement ((¬ p) ∨ q) ∨ (p ∧ (¬ q)) is a tautology asked in Discrete Mathematics byThe arguments of "≡" (the material equivalence sign) are called equivalentsHow to Tell if the Structure of a Logical Argument is Valid




The Negation Of P Q To R Is




Without Using Truth Tables Show That I P Q P P Q Ii P Q P Q Q R Q R
If statement forms P and Q are logically equivalent, then P Q is a tautology Conversely, if P Q is a tautology, then P and Q are logically equivalent Use to convert each of the logical equivalences to a tautology Then use a truth table to verify each tautologyAlgebra questions and answers p ↔ (p ∧ r) ≡ ¬p ∨ r Use the laws of propositional logic to prove the following (a) ¬p → ¬q ≡ q → p Solution ¬p → ¬q ¬¬p ∨ ¬q Conditional identity p ∨ ¬q Double negation law ¬q ∨ p Commutative law q → p Conditional identityFrom column (VII) and (VIII), we get p ∨ (q ∧ r) ≡ ( p ∨ q) ∧ ( p ∨ r) Concept Logical Connective, Simple and Compound Statements Report Error Is there an error in this question or solution?




Homework 2 Answer




Omtex Classes Chapter 1 Mathematical Logic State Which Of The Following Sentences Is A Statement Justify Your Answer If It Is A Statement Write Down Its Truth Value
The entries in columns 5 and 8 are identical ∴ p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r) Concept Statement Patterns and Logical Equivalence Report Error P ↔ Q may be less familiar, but it still makes intuitive sense It's another biconditional, Harriet will go if and only if Gloria doesn't go P ↔ ¬Q After all, P ↔ Q says P and Q have the same truth value P ↔ ¬Q says that P and ¬Q have the same truth value, that is, that P and Q have different truth values(p^q)^r≡p^(q^r) 1 See answer natsudragoneel444 is waiting for your help Add your answer and earn points



Logic Formal Proof For P Q P Q In Fitch Stack Overflow



2
∴ (∼p∧ ∼q)∨(p∧q)∨(r∧ ∼r) ≡∼((p∨q)∧ ∼(p∧q)) Note that if you apply the rules in reverse, you can go in the other direction (LHS to RHS) 2 2 Verifying Arguments The process of proving an argument is valid has a similar feel to proving logical equivalences, but2 여러 가지 정리나 명제를 진리표로 그 진위를 밝힐 수가 있는가?Chapter 11 Mathematical Logic Long Answers III Q 2 Q 1 Q 3



Propositional Logic 1 Propositions A Propositionis A Declarative



Solved 2 Show That Q P R Q R Q P A Chegg Com
The logical statement ∼(∼p∨q)∨(p∧r)∧(∼q∧r) is equivalent to A (p∧r)∧∼q B (∼p∧∼q)∧r C ∼p∨r D (p∧∼q)∨r Medium Solution Verified by Toppr Correct option is A) s∼(∼p∨q)∧(p∧r)∧(∼q∧r) ≡(p∧∼q)∨(p∧r)∧(∼q∧r) ≡p∧(∼q∨r)∧(∼q∧r) ≡p∧(∼q∧r) ≡(p∧r)∼q Was this answer helpful?• p ∧q ∨r means (p ∧q) ∨r rather than p ∧(q ∨r) • p ∨q → r is the same as (p ∨q) → r Logic and Bit Operations A bit is a symbol with two possible values, namely, 0 (zero) and 1 (one) the precedence levels of the logical operators, ¬, ∧, ∨, →, and ↔ Computer bitQuestion ¬p → (q → r) ≡ q → (p ∨ r) using the laws of logic to prove logical equivalence ex Use the laws of propositional logic to prove the following (a) ¬p → ¬q ≡ q → p Solution ¬p → ¬q ¬¬p ∨ ¬q Conditional identity p ∨ ¬q Double negation law ¬q ∨ p Commutative law q → p Conditional identity




Cs100 Discrete Structures Ppt Download



2
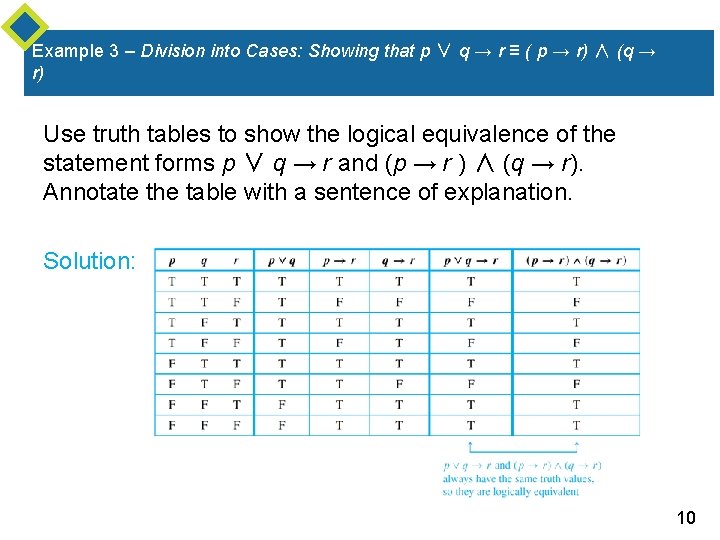
As (q ^ r) is common to both of these expressions, you are effectively saying that ~p ^ (~q ^ r) v (p ^ r) ≡ ~p ^ (p ^ r) v (~q ^ r) which is NOT the caseExample 213 p_q!r Discussion One of the important techniques used in proving theorems is to replace, or substitute, one proposition by another one that is equivalent to it In this section we will list some of the basic propositional equivalences and show how they can be 1 I came across this problem, it asks to use logical equivalences (see image), show that ( p → r) ∨ ( q → r) logically equivalent to the statement ( p ∧ q) → r (aka definition of biconditional) After apply p → q ≡ ¬ p ∨ q, I can't go any further can anyone show me any steps further?



How To Show That P Implies Q Implies R Is Equivalent To P And Q Implies R Quora




Using The Truth Table Prove The Following Logical Equivalence P Q P Q P Q
Ex 93, 5 (a) Add p (p – q), q (q – r) and r (r – p) Simplifying expressions p (p – q) = p × p – p × q = p2 – pq2 q (q – r) = q × q – q × r = q2 – qr r (r – p) = r × r – r × p = r2 – rp So, our answer is p2 q2 r2 – pq – qr – rp Show More Sabiendo que p→q≡﹁p∨q (p∨q )→r ≡ ﹁ (p∨q )∨r ≡ (p∧q)∨r por De Morgan ≡ (p∨r)∧ (q∨r) por distributividad ≡ (p→r ) ∧ ( q→r ) por De Morgan A Niccherip5 y otros 5 usuarios les ha parecido útil esta respuesta heart outlined heart outlined Gracias 5Prove p^ (qVr) and (p^ q)V(p^r) are logically equivalent written 53 years ago by teamques10 ★



9 If And Only If Using Theorems A Concise Introduction To Logic




Assignment1 Mth110
CMSC 3 Section 01 Homework1 Solution CMSC 3 Section 01 Homework1 Solution 1 Exercise Set 11 Problem 15 Write truth table for the statement forms (5 points) ~(p ^ q) V (p V q) El valor de verdad de la proposición compuesta ( ~p→q)∧ (q→r)∧ (~r) p es Verdadero, por lo tanto es un Tautologia Tabla de verdad es una tabla que muestra el valor de verdad de una proposición compuesta, para cada combinación de verdad que se pueda asignar18k modified 10 weeks ago by pedsangini276 ★




The Foundations Logic And Proofs Ppt Download
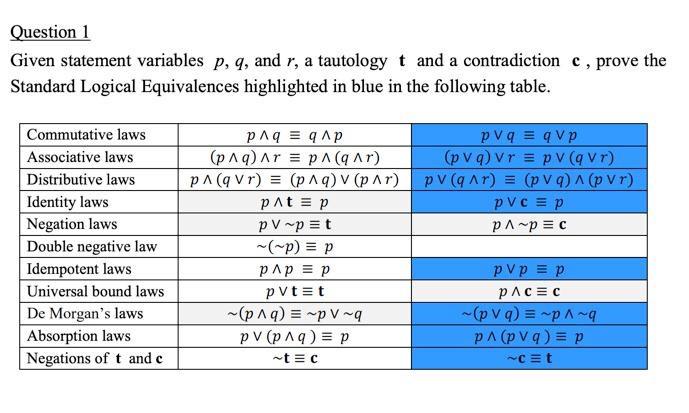



Solved Question 1 Given Statement Variables P Q And R A Chegg Com
Distributive laws p ∨ ( q ∧ r ) ≡ ( p ∨ q) ∧ ( p ∨ r ) p ∧ ( q ∨ r ) ≡ ( p ∧ q) ∨ ( p ∧ r ) Reformulate conjunctions and disjunctions within logical proofs Domination laws p ∧ F ≡ F p ∨ T ≡ T The conjunction with a proposition that is false is always false The3 배리법 (p→q)⇔(p∧∼q)→c 4 이출법칙 (p∧q→r)≡p→(q→r) 5 (p→r)∨(q→s)≡(p∧q→r∨s) 종합정리 1 항진, 함의 , 항위, 두 명제가 동치라는 용어의 뜻을 아는가?ICS 141 Discrete Mathematics I (Fall 14) 13 Propositional Equivalences Tautologies, Contradictions, and Contingencies A tautology is a compound proposition which is always true



How To Construct The Truth Table Of P Q Quora




Logical Equivalences
Answer (1 of 3) We can prove this with a Separation of Cases over r and \neg r Starting with the lefthand side 1 Suppose (p \lor \neg r) \land (q \lor r) 2 p \lor \neg r, from 1 (Conjunction Elimination) 3 q \lor r, from 1 (Conjunction Elimination) 4 CASE 1 Suppose r 5 1 \neg \neg r,Host A (on TCP/IP v4 network A) sends an IP datagram D to host B (also Which of the following is/are true?Submit order and get a quick answer at the best price for any assignment or question with DETAILED EXPLANATIONS!




Show That Each Of These Conditional Statements Is A Tautolog Quizlet



1 1 Propositional Logic Engineering Libretexts
Prove that p (¬ q ∨ r) ≡ ¬ p ∨ (¬ q ∨ r) using truth table asked in Discrete Mathematics by Anjali01 ( 478k points) discrete mathematics ~(p∨~q)↔ ~r Thus, they are equivalent Proved Related Answers Prove that (1 * 2) (2 * 3) (3 * 4) (4 * 5) n (n 1) = n (n 1) (n 2) / 3 for n positive integers In a survey, 00 people were queried if they read India Today or Business Times It was found 10 read India Today, 900 read Business Times and 400 read both2 第1 章 論理と証明 p q ¬p ¬q p−→q ¬q−→¬p t t f f t t t f f t f f f t t f t t f f t t t t 命題p−→qが真であるとき,p はqであるための十分条件,qはp であるための必要条件であるという.例 えば,命題「x= 1 ならばx2 = 1 である」は真であるから,「x= 1 である」は「x2 = 1 である」ための十分条件,




Logic Prove P Q R P Q P R From P Q R Using Natural Deduction Mathematics Stack Exchange




Propositional Logic Irina Prosvirnina Propositions Compound
Question The property p∧(q∨r)≡(p∧q)∨(p∧r) is called A associative law B commutative law C distributive law D idempotent law Medium Solution Verified by Toppr Correct option is C) As the symbol AND ∧ is distributed over OR ∨ , the given property is also called Distributive property Was this answer helpful?(¬ (p ∧q)) →(¬ p ∨q) ≡(¬ p ∨q) ?This tool generates truth tables for propositional logic formulas You can enter logical operators in several different formats For example, the propositional formula p ∧ q → ¬r could be written as p /\ q > ~r, as p and q => not r, or as p && q > !r The connectives ⊤ and ⊥ can be entered as T and F
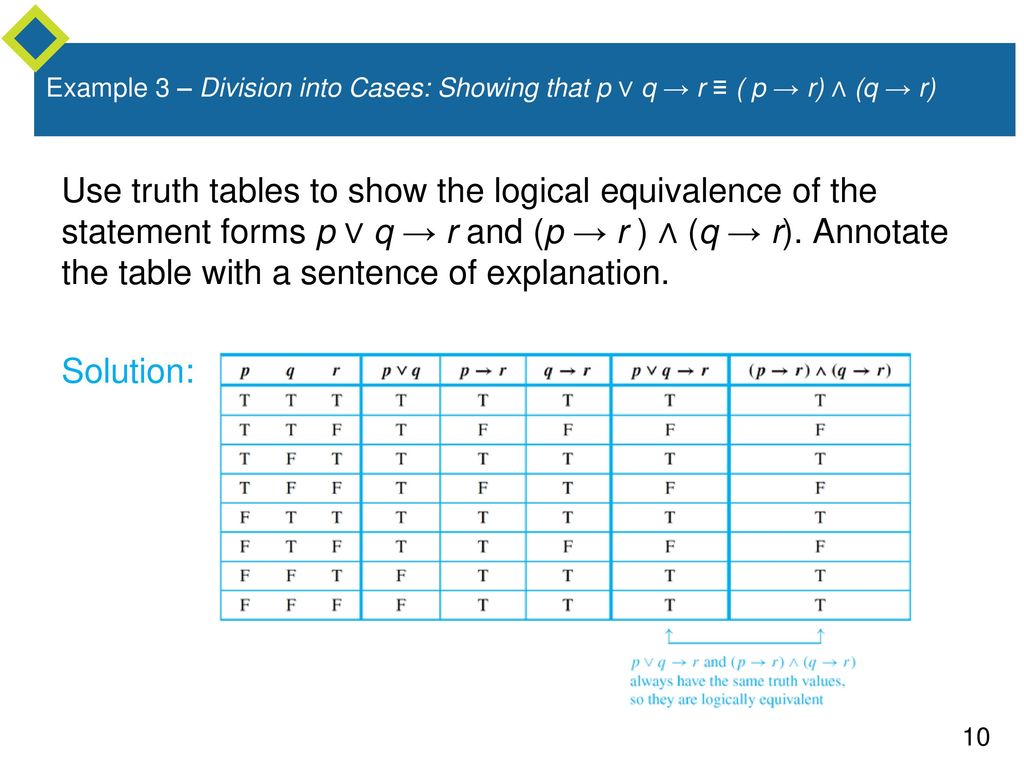



Conditional Statements Ppt Download




Cs 103 Discrete Structures Ppt Download
Thank you Image logical equivalencesP⇒(q⇔r)≡(p⇒q)⇔(p⇒r) (p⇒(q⇔r)≡(p⇒q)⇔(p⇒r)) CNF, DNF, truth table calculator, logical equivalence generator THERE'S THE ANSWER!3 연역적 추론이란 무슨




Proof And Problem Solving Truth Table Example 02 Youtube



2
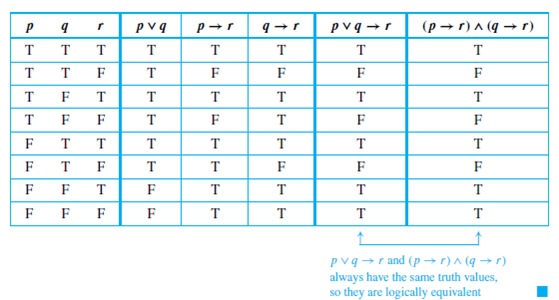
(p ⊕ q) ∧ r (p ⊕q)∧r and (p ∧ r) ⊕ (q ∧ r) (p∧r)⊕(q ∧r) have the same truth value in all cases, they are logically equivalent It follows that (p ⊕ q) ∧ r ≡ (p ∧ r) ⊕ (q ∧ r) (p ⊕q) ∧r ≡ (p∧r)⊕(q ∧r) Need a fast expert's response? If p or q are false the statement (P^Q)> R will always be true The same can be said for the statement (P > R) V (Q > R) If the first statement in P>Q is false then P >Q will always be true #4 JeremyHorne 19 0 tauon is right about the typo Adding a step or so will reveal why Original (¬P V R) V (¬Q V R) = (¬P ∧ ¬Q) V R NewIn a system the contents of PC, Base register, Register R1, and Regist struct ListNode *function (struct ListNode *head) { struct ListNode *




Tutorial 1 Solution




Short Truth Table Method Determine The Validity Using The Short Truth Table Method P Q R S Q S Pvr Homeworklib
Tabel kebenaran untuk ekspresi p → q dengan ~p v q Karena untuk tiaptiap baris, nilai kebenaran pada kolom p → q dan ~p v q sama, maka disimpulkan bahwa p → q ≡ ~p v q Contoh buktikan ekuivalensi tanpa menggunakan tabel kebenaran dari (q → p) ≡ (~p → ~q), karena persamaan kanan lebih komplek maka kita turunkan\begin{array}{cccccccccccccccccc}p&q&r&p \supset q&q\supset r0 0 Similar questions
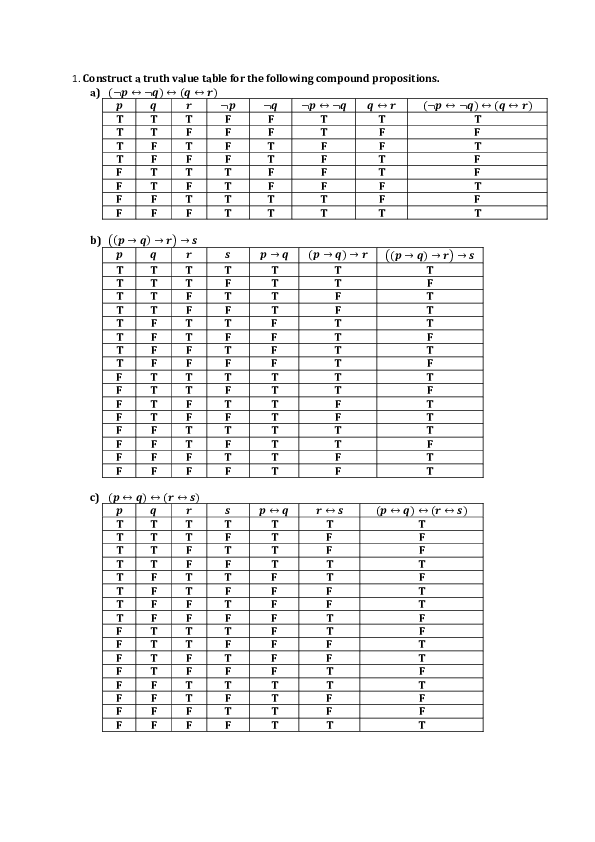



Doc Assignment Caroline Murthy Academia Edu
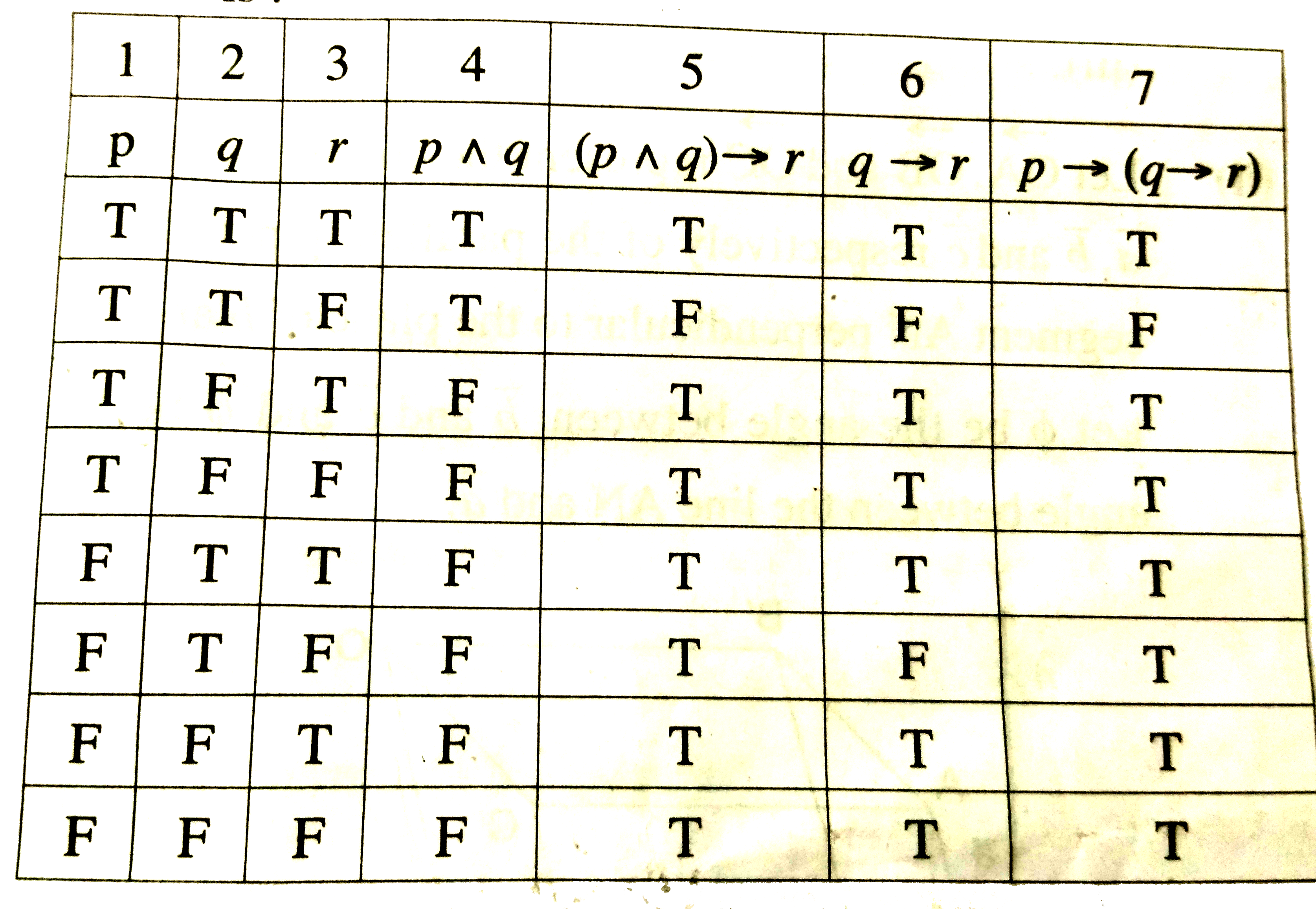



Using Truth Table Prove The Following Logical Equivalence P Q Rarr R P Rarr Q Rarr R
Finally, p ≡ q (" p is materially equivalent to q " or " p if and only if q ") is to count as true when p and q have the same truth value (ie, either when both are true or when both are false), and false when they have different truth values;




Solved P Q Q R P R Developing A Chain Of Chegg Com



What Is The Reasoning Behind The Truth Table For Implies Math P To Q Math In Particular Why Does Math P To Q Math True When P Is False Quora




17th Parts Logic Equiv P Q P R P Q R Youtube




Logic And Proofs




Using Truth Table Prove The Following Logical Equivalence P Q Rarr R P Rarr Q Rarr R Youtube




Use Truth Tables To Verify The Associative Laws A P Q Quizlet



Discrete Mathematics Unit 1 Set Theory And Logic




Logic Show That P Q Q R Is Equivalent To P R P Q R Q Mathematics Stack Exchange



Biconditional Truth Table




Prepare The Truth Table Of The Following Statement Patterns I P Q Q P Ii P Q P Iii P Q P Q Iv P R Q P V P Q R P




Without Using Truth Table Show That P Q P Q P Q




Solved 2 Show That Q P R Q R Q P A Chegg Com



Using Truth Tables Prove The Following Logical Equivalences P Q P Q Q P Sarthaks Econnect Largest Online Education Community




Construct A Truth Table For Each Of These Compound Propositi Quizlet




Show That P Q And P Q Are Logically Equivalent Slader




Logic Truth Table For P Q R Q Youtube




If The Statements P And Q Are True And The Statement R And S Are False Find The Truth Values Of 1 Pvvq R Pvvq Vv R Vvs 2 P Q P R Vv S Vv R



6 Conditional Derivations A Concise Introduction To Logic




Solved Question 1 Given Statement Variables P Q And R A Chegg Com



2



Show That P Q And P Q Are Logically Equivalent Slader



Answer In Discrete Mathematics For Muhammad Abdullah 1713



1




Logic Show That P Q Q R Is Equivalent To P R P Q R Q Mathematics Stack Exchange




Show That P Q And P Q Are Logically Equivalent Slader



Conditional Statements Let P And Q Be Statements




Pdf Rules Of Logical Inference Dr Jason J Campbell Academia Edu




Discrete Mathematics Proving P To Q Land P To R Equiv P To Q Land R Using Logic Laws Short Cut Or Incorrect Mathematics Stack Exchange



How To Simplify P Q P R Q R Quora




P Implies R Q Implies R Conclusion P Or Q Implies R Show They Sre Homeworklib



2



Reading Chapter 4 44 59 From The Text Book Ppt Video Online Download



Truth Table Generator



2



Show That P Q Q R P R Is A Tautology By Using The Rules




Logic Truth Table For P Q R Q Youtube




Logic Show That P Q Q R Is Equivalent To P R P Q R Q Mathematics Stack Exchange




Show That P Q Q R P R Is A Tautology By Using The Rules




Word Version



The Statement P P Q Q R R Is 1 A Tautology 2 Equivalent To P R 3 A Fallacy 4 Equivalent To Q R Sarthaks Econnect Largest Online Education Community




Discrete Mathematics Unit 1 Set Theory And Logic



Prove P Q R P Q R Without Using Truth Table Sarthaks Econnect Largest Online Education Community




If Statement P Q Q R Is False Then Truth Values Of Statements P Q R Respectively Can Be




Propositional Logic Irina Prosvirnina Propositions Compound




Part 1 Math170 E Portfolio




Csc 102 Discrete Structures Lecture Ppt Download




If The Statements P And Q Are True And The Statement R And S Are False Find The Truth Values Of 1 Pvvq R Pvvq Vv R Vvs 2 P Q P R Vv S Vv R
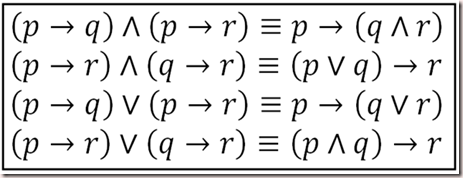



Stpm Further Mathematics T 1 1 Logic



2




Truth Table Questions And Answers



Prove That P Q R P Q R Using Truth Table Sarthaks Econnect Largest Online Education Community



Show That Pvvq Vvr Harr Pvv Qvvr Is A Tautology



How To Construct The Truth Table Of P Q Quora




Part 1 Math170 E Portfolio




01 Proposition Logic And Propositional Equivalences Discrete Mathematics Explained In Detail



Solved Let P Q R Q And P R A Use Truth Table Method To Determine Whether B Use Propositional Resolution To Determine Whether Hin Course Hero




Logic Show That P Q Q R Is Equivalent To P R P Q R Q Mathematics Stack Exchange




Formal Logic The Propositional Calculus Britannica




Discrete Mathematics Unit 1 Set Theory And Logic




Logic And Proofs



Show That P Q Q R P R Is A Tautology By Using The Rules




Which Of The Following Is Logically Equivalent To P Q



2



Solved Use The Logical Equivalence Established In Example To Rew Chegg Com




Example 4 Show That Points P 2 3 5 Q 1 2 3 And R 7 0 1



Using Truth Tables Prove The Following Logical Equivalences 1 P Q P Q 2 P Q P Q P Q Sarthaks Econnect Largest Online Education Community




Solved Use The Laws Of Logical Equivalence Theorem 2 1 1 On Chegg Com




How To Prove This Logical Statement P R Q R P R Q R Quora



1




Logic And Proofs




Chapter 2 The Logic Of Compound Statements Flashcards Quizlet




Copyright C Cengage Learning All Rights Reserved Chapter 2 The Logic Of Compound Statements The Logic Of Compound Statements Ppt Download


